표준정규분포
평균 $\mu$, 표준편차 $\sigma$인 정규분포의 확률밀도 함수는 아래와 같습니다.
$n(x;\mu,\sigma) = \frac{1}{\sqrt{2\pi}\sigma}e^{\frac{1}{2\sigma^{2}}(x-\mu)^{2}}$
정규분포의 확률을 구하는 방법
$P(x_{1} < X < x_{2}) = \int_{x_{1}}^{x_{2}}n(x;\mu, \sigma)dx= \frac{1}{\sqrt{2\pi}\sigma}\int_{x_{1}}^{x_{2}}e^{-\frac{1}{2\sigma^{2}}(x-\mu)^{2}}dx$
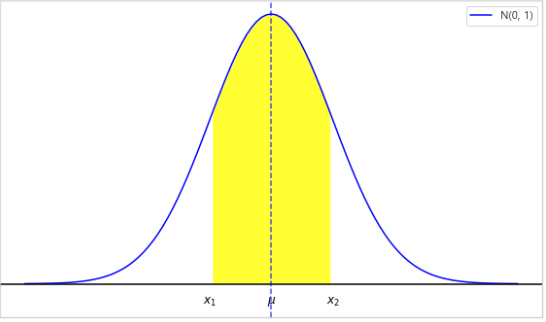
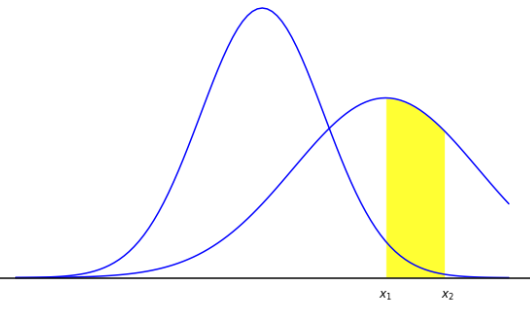
모든 정규확률변수 $X$를 평균이 0이고 분산이 1인 정규확률변수 $Z$로 변환할 수 있습니다.
$Z = \frac{X-\mu}{\sigma}$
$X$가 $x$ 값을 취할 때 대응하는 Z 값은 $z = \frac{x-\mu}{\sigma}$입니다.
평균이 $\mu$이고 분산이 $\sigma^{2}$인 정규확률변수 X가 어떤 구간의 값을 취할 확률을 평균이 0이고
분산이 1인 정규확률변수를 이용하여 구할 수 있습니다.
$P(x_{1} < X < x_{2}) = \frac{1}{\sqrt{2\pi}\sigma}\int_{x_{1}}^{x_{2}}e^{-\frac{1}{2\sigma^{2}}(x-\mu)^{2}}dx = \frac{1}{\sqrt{2\pi}}\int_{z_{1}}^{z_{2}}e^{-\frac{1}{2}z^{2}}dz = \int_{z_{1}}^{z_{2}}n(z;0,1)dz = P(z_{1} < Z < z_{2})$
$z_{1} = \frac{x_{1} - \mu}{\sigma}$, $z_{2} = \frac{x_{2} - \mu}{\sigma}$
평균이 0이고 분산이 1인 정규확률변수의 분포를 표준정규분포(standard normal distribution)이라 합니다.
정규곡선 아래의 면적을 구할 때는 표준정규곡선에 대한 표를 이용합니다.
표는 인터넷 상에서 얼마든지 찾아볼 수 있습니다.
유니와이즈 수리통계학의 내용을 바탕으로 요약 작성되었습니다.
'수리통계학 > 연속형 확률분포' 카테고리의 다른 글
| 카이제곱 분포 (0) | 2019.09.26 |
|---|---|
| 감마분포와 지수분포 (0) | 2019.09.24 |
| 감마함수 (0) | 2019.09.20 |
| 정규분포 - 평균과 분산 증명 (0) | 2019.09.16 |
| 정규분포 - 개념 (0) | 2019.09.11 |


댓글