군집
군집은 데이터셋을 클러스터라는 그룹으로 나누는 작업입니다.
한 클러스 안의 데이터 포인트는 매우 비슷하고 다른 클러스터의 데이터 포인트와는 구분되도록 데이터를 나누는 것이 목표입니다.
군집은 탐색적 도구이며, 의미있는 군집들을 형성할 때만 유용합니다.
데이터가 속한 군집이 "실제" 군집이라고 명확하게 말할 수는 없습니다. 우연한 결과일수도 있다는 점을 명심합니다.
군집은 데이터를 이해하고 요약하는 데 쓰입니다.

K-평균 군집
k-평균 군집은 가장 간단하고 또 널리 사용하는 군집 알고리즘입니다.
데이터의 어떤 영역을 대표하는 클러스터 중심을 찾습니다.
알고리즘은 두 단계를 반복합니다.
먼저 데이터 포인트를 가장 가까운 클러스터 중심에 할당하고
클러스터에 할당된 데이터 포인트의 평균으로 클러스터 중심을 다시 지정합니다.
유클리디안 거리가 기본 값으로 사용됩니다.
클러스터에 할당되는 데이터 포인트에 변화가 없을 때 알고리즘이 종료됩니다.
K-평균 군집 예시
삼각형은 클러스터 중심이고 원은 데이터 포인트입니다.
클러스터는 색으로 구분했고 3개의 클러스터를 찾도록 지정했습니다.
mglearn.plots.plot_kmeans_algorithm()
주요 하이퍼파라미터 : 클러스터 K의 개수

하이퍼파라미터 K의 효과 (n_clusters)

클러스터의 개수를 다르게 하여 k-평균 군집을 이용한 클러스터 할당입니다.
무작위 초기화 효과
초기화를 무작위로 하기 때문에 알고리즘을 다시 실행하면 클러스터의 번호가 다르게 부여될 수 있습니다.

Blobs 데이터셋 예시 - KMeans
from sklearn.datasets import make_blobs
X_train, _ = make_blobs(random_state=1)
print("X_train.shape:", X_train.shape)
Blobs 데이터셋을 불러오고 X_train의 형태를 살핍니다.
from sklearn.cluster import KMeans
kmeans = KMeans(n_clusters=3)
kmeans.fit(X_train)
KMeans의 객체를 생성하고 클러스터의 수를 3으로 지정합니다. 그런 다음 fit 메서드를 호출합니다.
print(kmeans.cluster_centers_)
클러스터 중심입니다.
assignments_X_train = kmeans.labels_
print(assignments_X_train)
kmeans.labels_ 속성에서 레이블을 확인할 수 있습니다.
X_new, _ = make_blobs()
assignments_X_new = kmeans.predict(X_new)
print(assignments_X_new)
predict 메서드를 사용해 새로운 데이터의 클러스터 레이블을 예측할 수 있습니다.
예측은 각 포인트에 가장 가까운 클러스터 중심을 할당하는 것이며 기존 모델을 변경하지 않습니다.
mglearn.discrete_scatter(X[:, 0], X[:, 1], kmeans.labels_, markers='o')
mglearn.discrete_scatter(
kmeans.cluster_centers_[:, 0], kmeans.cluster_centers_[:, 1], [0, 1, 2],
markers='^', markeredgewidth=2)
그래프로 표현했습니다.
군집 알고리즘의 비교와 평가
군집 알고리즘의 결과를 실제 정답 클러스터와 비교하여 평가할 수 있는 지표들이 있습니다.
1 (최적일 때) 과 0 (무작위로 분류될 때) 사이의 값을 제공하는 ARI 지표가 있습니다.
adjusted_rand_score 함수를 사용합니다.
from sklearn.metrics.cluster import adjusted_rand_score
adjusted_rand_score([0, 0, 1, 1], [0, 0, 1, 1])
adjusted_rand_score([0, 0, 1, 1], [1, 1, 0, 0])
완벽하게 매칭된 레이블의 점수는 1입니다.
adjusted_rand_score([0, 0, 1, 2], [0, 0, 1, 1])
adjusted_rand_score([0, 0, 0, 0], [0, 1, 2, 3])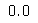
아이리스 데이터셋 예시 - KMeans
from sklearn.datasets import load_iris
iris = load_iris()
X_train, y_train = iris.data, iris.target
print("X_train.shape:", X_train.shape)X_train.shape: (150, 4)
데이터셋을 불러오고 형태를 살펴봅니다.
from sklearn.cluster import KMeans
kmeans = KMeans(n_clusters=3)
kmeans.fit(X_train)
KMeans의 객체를 생성하고 클러스터의 수를 3으로 지정한 후 fit 매서드를 호출합니다.
print(kmeans.cluster_centers_)
클러스터 중심입니다.
from sklearn.metrics import adjusted_rand_score
assignments_X_train = kmeans.labels_
print('adjusted_rand_score :', adjusted_rand_score(y_train, assignments_X_train))
실제 정답 클러스터랑 비교하여 평가했습니다.
아이리스 데이터셋 예시 (스케일링) - KMeans
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
X_train_scaled = scaler.fit_transform(X_train)
스케일링 해주었습니다.
from sklearn.cluster import KMeans
kmeans = KMeans(n_clusters=3)
kmeans.fit(X_train_scaled)
모델을 만듭니다.
print(scaler.inverse_transform(kmeans.cluster_centers_))
클러스터 중심입니다.
from sklearn.metrics import adjusted_rand_score
assignments_X_train_scaled = kmeans.labels_
print('adjusted_rand_score :', adjusted_rand_score(y_train, assignments_X_train_scaled))adjusted_rand_score : 0.6201351808870379
스케일 후 점수가 더 낮아졌습니다.
결론
K-평균의 주요 하이퍼파라미터
n_clusets (클러스터 k의 개수)
데이터 전처리 과정이 중요합니다.
장점
K-평균은 비교적 이해하기 쉽고 구현도 쉽습니다.
빠릅니다.
단점
무작위 초기화를 사용하여 알고리즘의 출력이 초깃값에 따라 달라집니다.
찾으려 하는 클러스터의 개수를 지정해야합니다 (실제 애플리케이션에서는 알 수 없을 것입니다).
성능이 데이터 스케일링에 의존합니다.
클러스터의 모양을 가정하고 있어서 활용 범위가 제한적입니다.
K-평균 알고리즘이 실패하는 경우
각 클러스터를 정의하는 것이 중심 하나뿐이므로 클러스터는 둥근 형태로 나타납니다.
복잡한 형태의 클러스터라면 성능이 나빠집니다.
클러스터의 개수를 정확하게 알고 있더라도 k-평균 알로리즘이 이를 항상 구분해낼 수 있는 것이 아닙니다.


파이썬 라이브러리를 활용한 머신러닝 책과 성균관대학교 강석호 교수님 수업 내용을 바탕으로 요약 작성되었습니다.
'파이썬 라이브러리를 활용한 머신러닝' 카테고리의 다른 글
| DBSCAN (0) | 2019.11.28 |
|---|---|
| Hierarchical Clustering (0) | 2019.11.26 |
| t-distributed Stochastic Neighbor Embedding (0) | 2019.11.19 |
| Principal Component Analysis (0) | 2019.11.18 |
| Unsupervised Learning & Data Preprocessing (0) | 2019.11.15 |




댓글