▶ $\beta_{1}$의 해석
로지스틱 회귀에서 $\beta_{1}$의 의미를 해석하는 일은 쉽지 않습니다.
Y가 아닌 P(Y)를 예측하기 때문입니다.
만약 $\beta_{1} = 0$라면, Y와 X 사이에 관계가 없다는 뜻입니다.
만약 $\beta_{1} > 0$일 때, X가 커지면 Y = 1일 확률도 커집니다.
만약 $\beta_{1} < 0$일 때, X가 커지면 Y = 1일 확률은 작아집니다.
얼마나 더 큰지 작은 지는 기울기에 따라 의존합니다.
▶ 계수가 중요할까?
로지스틱 회귀에서 가설 검정을 시행합니다. $\beta_{0}$, $\beta_{1}$이 0이 아니라고 확신할 수 있는지를 봅니다.
여기서는 T test 대신 Z test를 사용합니다. 그렇다고 p-value 해석하는 방법이 바뀌진 않습니다.
아래의 그림에서 p-value는 매우 작고 $b_{1}$은 양수입니다. 따라서 balance가 증가하면
default 확률도 증가한다고 볼 수 있습니다.

▶ 예측하기
한 사람의 average balance가 1000일 때, default의 확률은 어떻게 될까?
$\hat{p}(X) = \frac {e^{\hat {\beta_{0}}+\hat {\beta_{1}}X}}{1 + e^{\hat {\beta_{0}}+\hat {\beta_{1}}X}} = \frac {e^{-10.6513 + 0.0055 \times 1000}}{1 + e^{-10.6513 + 0.0055 \times 1000}} = 0.00576$
이 사람의 예측 default 확률은 1% 미만입니다.
balance가 2000일 때, 확률은 더 높아져 0.586(58.6%)가 됩니다.
▶ 로지스틱 회귀가 정성적(Qualitative) 예측변수를 가질 경우
individual default를 학생인지 아닌지를 체크해서 예측하려고 합니다.
qualitative variable "Student"를 코드화 합니다
(Student = 1, Non-student = 0)
$b_{1}$은 양수입니다. 학생이 더 높은 default probabilities 경향을 보입니다.


▶ 다중 로지스틱 회귀
선형 회귀 처럼 다중 로지스틱 적합도 가능합니다.
$p(X) = \frac{e^{\beta_{0}+\beta_{1}X_{1} + \cdots + \beta_{p} X_{p}}}{1 + e^{\beta_{0}+\beta_{1} X_{1} + \cdots + \beta_{p} X_{p}}} $
▶ 다중 로지스틱 회귀 - Default Data
Predict Default using
Balance (quantitaive)
Income (quantitative)
Student (qualitative)

▶ 예측
credit card balance $1,500, income $40,000, student
default 확률 측정하기
$\hat{p}(X) = \frac {e^{-10.8690.00574 \times 1500 + 0.003 \times 40 - 0.6468 \times 1}}{1 + e^{-10.8690.00574 \times 1500 + 0.003 \times 40 - 0.6468 \times 1}} = 0.058$
▶ 다중 로지스틱 회귀를 적합했을 때 명백히 다른 점

▶ Students(Orange) vs Non-students(Blue)
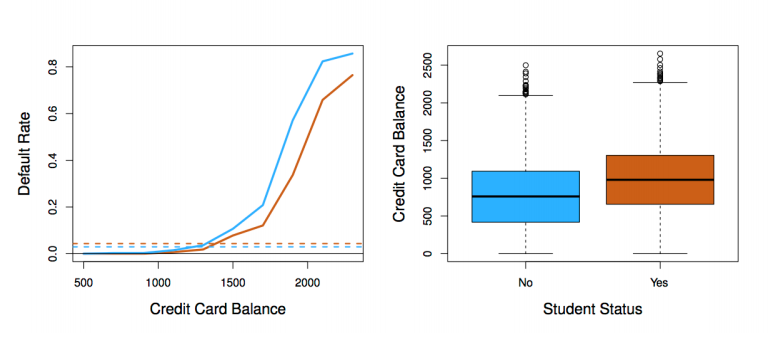
▶ 누구에게 신용을 제공해야 할까?
credit card balance is available에 대한 아무런 정보가 없다면 학생은 학생이 아닌 사람보다 더 리스크가 크다.
그러나 같은 credit card balance에서는 학생이 리스크가 더 작습니다.
'ISLR' 카테고리의 다른 글
| Ch05 Resampling Methods - The Validation Set (0) | 2019.09.26 |
|---|---|
| Ch04 분류분석(3) - LDA & QDA (0) | 2019.09.25 |
| Ch04 분류분석(1) (0) | 2019.09.23 |
| Chap3 회귀분석(3) (0) | 2019.09.20 |
| Chap3 회귀분석(2) (0) | 2019.09.19 |




댓글