정규분포 확률밀도함수
정규분포의 확률밀도함수는 다음과 같습니다.
$n(x;\mu, \sigma) = \frac {1}{\sqrt {2\pi}\sigma} e^{-\frac {1}{2\sigma^{2}}(x-\mu)^{2}}$, $-\infty < x < \infty$
정규분포 그래프 그리기(함수 사용)
import numpy as np
# numpy.linspace(start, stop, num=50, endpoint=True, retstep=False, dtype=None, axis=0)
# start = -10, stop = 10, num = 101)로 설정
x = np.linspace(-10, 10, 101) # x 정의
x
x의 범위는 -10부터 10까지 100 등분하였습니다.
# numpy.exp(x, /, out=None, *, where=True, casting='same_kind', order='K', dtype=None, subok=True[, signature, extobj]) = <ufunc 'exp'>
# numpy.sqrt(x, /, out=None, *, where=True, casting='same_kind', order='K', dtype=None, subok=True[, signature, extobj]) = <ufunc 'sqrt'>
# 표준정규분포
f_x = (1 / np.sqrt(2 * np.pi)) * np.exp(- x ** 2 / 2 )
f_x
정규분포 공식으로 계산할 결과입니다.
표준 정규분포이기 때문에 $\mu = 0$, $\sigma = 1$입니다.
import matplotlib.pyplot as plt
%matplotlib inline
# matplotlib.pyplot.grid(b=None, which='major', axis='both', **kwargs)
plt.figure(figsize=(8, 6)) # 플롯 사이즈 지정
plt.plot(x, f_x)
plt.xlabel("x") # x축 레이블 지정
plt.ylabel("f_x") # y축 레이블 지정
# plt.grid() # 격자 보이기
plt.title("Normal Distribution without scipy") # 제목 표시
plt.legend(["N(0, 1)"]) # 범례 표시
plt.show() # 플롯 보이기
그래프를 그리면 위와 같습니다.
정규분포 그래프 그리기(scipy 사용)
import scipy.stats as stats
# scipy.stats.norm = <scipy.stats._continuous_distns.norm_gen object>[source]
f_x1 = stats.norm(0, 1).pdf(x)
print(f_x1)
plt.figure(figsize=(8, 6)) # 플롯 사이즈 지정
plt.plot(x, f_x1, color="purple") # 선 색깔 보라색
plt.xlabel("x") # x축 레이블 지정
plt.ylabel("f_x1") # y축 레이블 지정
# plt.grid() # 격자 보이기
plt.title("Normal Distribution with scipy.stats") # 제목 표시
plt.legend(["N(0, 1)"]) # 범례 표시
plt.show() # 플롯 보이기
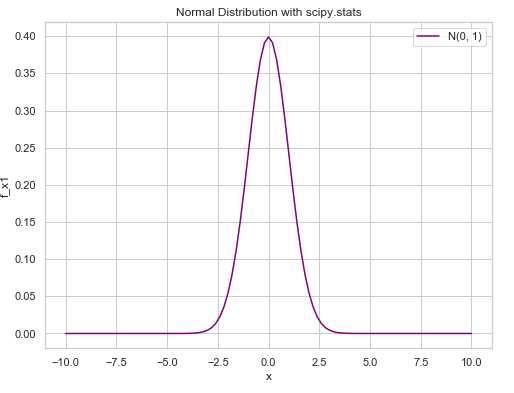
scipy.stats를 이용해 정규 분포를 계산하고 그래프를 그렸습니다.
결과가 거의 똑같이 나왔습니다. 실제 수식으로 계산한 것과 차이를 느끼지 못합니다.
정규분포 평균 변형
legend = []
def norm (mu, var) :
legend.append("N(" + str(mu) + ", " + str(var) + ")")
return stats.norm(mu, var).pdf(x)
plt.figure(figsize=(8, 6)) # 플롯 사이즈 지정
for i in np.arange(4) + 1:
plt.plot(x, norm(i, 1)) # plot 추가
plt.xlabel("x") # x축 레이블 지정
plt.ylabel("f_x3") # y축 레이블 지정
# plt.grid() # 격자 보이기
plt.title("Normal Distribution with scipy.stats") # 제목 표시
plt.legend(legend) # 범례 표시
plt.show() # 플롯 보이기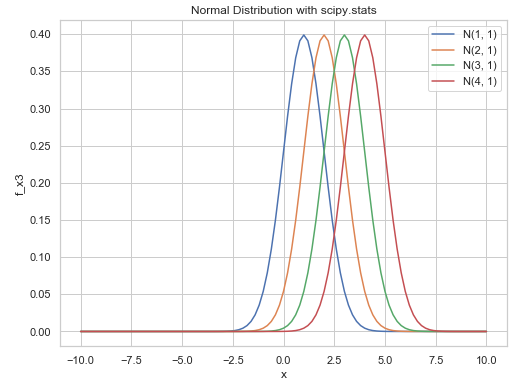
평균을 바꿔주면 중심 위치만 변화합니다.
정규분포 표준편차 변형
legend = []
def norm (mu, var) :
legend.append("N(" + str(mu) + ", " + str(var) + ")")
return stats.norm(mu, var).pdf(x)
plt.figure(figsize=(8, 6)) # 플롯 사이즈 지정
for i in np.arange(4) + 1:
plt.plot(x, norm(0, i)) # plot 추가
plt.xlabel("x") # x축 레이블 지정
plt.ylabel("f_x3") # y축 레이블 지정
# plt.grid() # 격자 보이기
plt.title("Normal Distribution with scipy.stats") # 제목 표시
plt.legend(legend) # 범례 표시
plt.show() # 플롯 보이기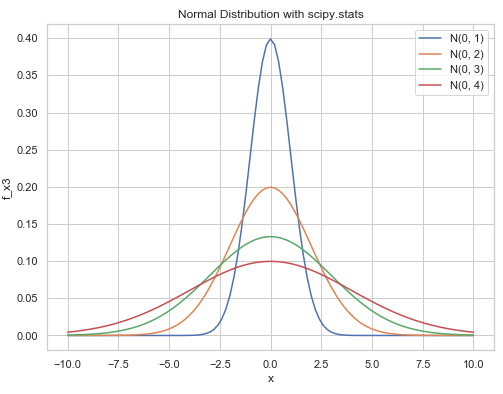
표준편차를 바꿔주면 중심 위치는 같고 퍼지는 정도가 달라집니다.
'Python > 통계' 카테고리의 다른 글
| 감마분포 with python (0) | 2019.10.14 |
|---|---|
| (2)정규분포의 누적분포함수를 python으로 구현해보자 (0) | 2019.08.22 |
| (1)정규분포 밀도함수 python 함수로 만들어보기 (0) | 2019.08.20 |

댓글