Tree-based Method
Tree-based method는 회귀와 분류 모두 가능합니다.
여러 simple regions로 predictor space를 계층화하거나 분해합니다.
위 과정이 트리 모양으로 요약되기 때문에 decision-tree 방법이라고 부릅니다.
Pros and Cons
Tree-based method는 간단하고 해석하기 쉽습니다.
예측 정확도에서 다른 최고의 지도 학습 접근법과는 뒤쳐지는 경향이 있습니다.
보완하기 위해 bagging, random forest, boosting을 사용합니다.
위의 보안법들은 트리들을 결합하는데 트리를 결합하는 것은 예측 정확도를 굉장히 높일 수 있지만
해석하기 다소 어렵게 됩니다.
Baseball salary data
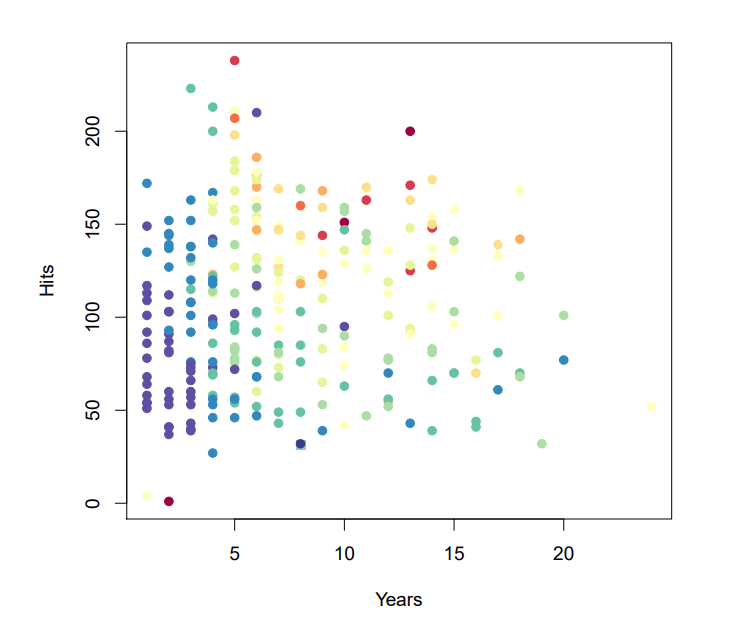
Salary가 낮으면 blue, green, 높으면 yellow, red입니다.
Decision tree for these data

위 데이터의 decision tree 입니다.
Details of previous figure
Hitters data에서 회귀 트리는 야구 선수의 log salary를 예측할 것입니다.
메이저리그에서 뛴 햇수와 이전 년도의 hits를 가지고 예측합니다.
Salary를 로그 변환해준 이유는 분포를 종모양으로 만들기 위해서입니다.
Internal node에서 label($X_{j} < t_{k}$의 형식)은 왼쪽의 branch를 나타내고 오른쪽 branch는 $X_{j} \geq t_{k}$을 나타냅니다.
위 트리는 두 개의 internal nodes와 세 개의 terminal nodes or leaves를 가집니다.
각 leaf의 숫자는 관측치에 해당하는 the mean of the response입니다.
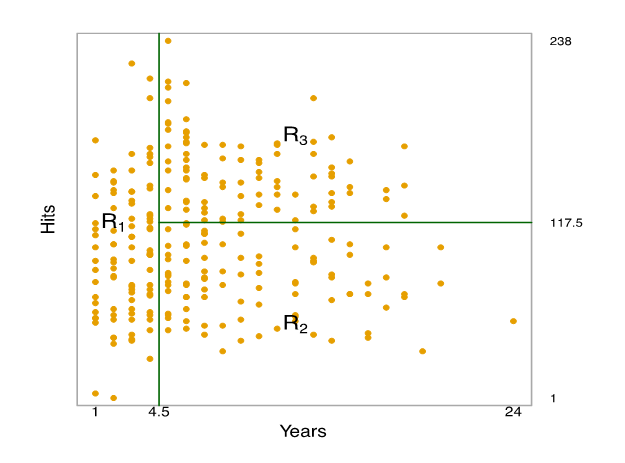
Result
전체적으로, 트리는 세 개의 예측 공간 영역에 속하는 players로 나뉩니다.
$R_{1} ={X | Years< 4.5}$, $R_{2} ={X | Years \geq 4.5, Hits <117.5}$, and $R_{3} ={X | Years \geq 4.5, Hits \geq 117.5}$.
Terminology for Trees
The regions $R_{1}, R_{2}, R_{3}$는 terminal node입니다.
트리는 아래로 뻗어 나갑니다.
The tree가 predictor space로 분리되는 지점은 internal nodes입니다.
위의 트리에서 두 개의 internal nodes는 Years<4.5 and Hits <117.5입니다.
Interpretation of Results
Years는 Salary를 결정하는데 가장 중요한 요소입니다. 경험이 덜 할수록 더 적은 salary를 받습니다.
경험이 덜하면 Hits의 수는 salary에 큰 역할을 하지 못합니다.
그러나 메이저리그의 경험이 5년 이상이면 Hits의 수는 salary에 영향을 미칩니다. 더 많이 치면 salary가 더 높습니다.
회귀 모델과 비교해서 실제 관계를 지나치게 단순화했지만 보기도, 해석하기도, 설명하기도 쉽습니다.
Partitioning Up the Predictor Space
회귀 문제에서 예측할 수 있는 한 가지 방법은 predictor space로 나누는 것이 있습니다.
즉, 모든 가능한 변수 $X_{1}, X_{2},..., X_{p}$를 겹치지 않는 distinct regions ($R_{1}, R_{2},..., R_{k}$)으로 넣는 것입니다.
특정 region $R_{j}$에 속한 모든 X에 동일한 예측을 합니다.
예측은 $R_{j}$에 속한 training 관측치의 평균 response values입니다.
예를 들어 두 개의 regions $R_{1}$, $R_{2}$ ($\hat{Y_{1}} = 10$, $\hat {Y_{2}} = 20$인)이 있다고 가정합니다.
어떤 $X$의 값이 $X \in R_{1}$라면 10을 예측할 수 있고, $X \in R_{2}$라면 20을 예측합니다.
More details of the tree-building process
이론적으로 영역은 어떤 모양이든 가질 수 있습니다.
그러나 예측 모델 결과 해석을 쉽게 하기 위해 predictor space를 high dimensional rectangles or boxes로 나누는 것만 선택합니다.
목표는 RSS를 최소화하는 boxes $R_{1}, ..., R_{J}$를 찾는 것입니다.
$\sum_{j=1}^{J}\sum_{i \in R_{j}}(y_{i} - \hat {y_{R_{j}}})^{2}$
$\hat{y_{R_{j}}}$는 j번째 box안 training 관측치들의 평균 response입니다.
모든 j번째 box의 분할을 고려하는 것은 무리입니다.
이러한 이유로 recusive binary splitting으로 알려진 top-down, greedy 접근법을 사용합니다.
Top-down은 꼭대기부터 시작해 연속적으로 predicotr space를 분할합니다.
각 분할은 두 개의 새로운 branch를 생성하고 아래로 퍼집니다.
Greedy는 트리가 만들어지는 과정에서 특정 단계에서 가장 좋은 분리가 일어나도록 합니다.
Perform Recursive Binary Splitting
The predictor $X_{j}$를 선택한 후 RSS를 가장 크게 줄일 수 있는 the predictor space을 가를 지점을 찾습니다.
계속해서 위 과정을 반복합니다. RSS를 최소화하는 가장 좋은 predictor와 cutpoint를 찾습니다.
그러나 전체 predictor space에서 분할하는 것이 아닌 이미 분할된 두 지역 중 하나를 분할합니다.
총 세 개의 지역이 만들어집니다.
세 개의 지역 중 한 개를 분할합니다. 이 작업은 분할을 멈출 때까지 계속됩니다.
예를 들어 다섯 개 이상의 관측치가 없는 지역이 생길 때까지 계속 진행합니다.
$R_{1}(j, s) = {X|Xj < s} and R_{2}(j, s) = {X|X_{j} ≥ s}$
다음 방정식을 최소화하는 j와 s의 값을 찾아야 합니다.

$\hat {y_{R_{1}}}은 $R_{1}(j, s)$ 안의 training 관측치의 the mean response입니다.
$\hat {y_{R_{2}}}는 $R_{2}(j, s)$ 안의 training 관측치의 the mean response
Feature p의 수가 그리 크지 않다면 위의 방정식을 최소화하는 j, s를 찾는 것은 빠르게 끝낼 수 있습니다.
Predictions
Test 관측치의 the response를 예측하기 위해선
test 관측치가 속하는 지역 안 training 관측치의 the response의 평균을 사용합니다.

맨 위 왼편 : Recursive binary splitting을 하지 않은 A partition of two-dimensional feature space입니다.
맨 위 오른편 : Recursive binary splitting을 한 a two-dimensional example입니다.
아래 왼편 : 맨 위 오른편에 대응하는 트리입니다.
아래 오른편 : 트리에 대응하는 a perspective plot of the prediction surface입니다.
The General View
두 개의 예측 변수가 있고 다섯 개의 distinct regions이 있습니다.
새로운 X가 어느 region에 속하느냐에 따라 다섯 개의 가능한 Y 값 중 하나를 택할 수 있습니다.

Splitting the X Variables
일반적으로 X 변수들 중 하나를 두 개의 regions으로 반복해서 분리하여 partitions을 만듭니다.

1. $X_{1} = t_{1}$으로 분리합니다.

2. 만약 $X_{1} < t_{1}$이면, $X_{2} = t_{2}$를 분리합니다.
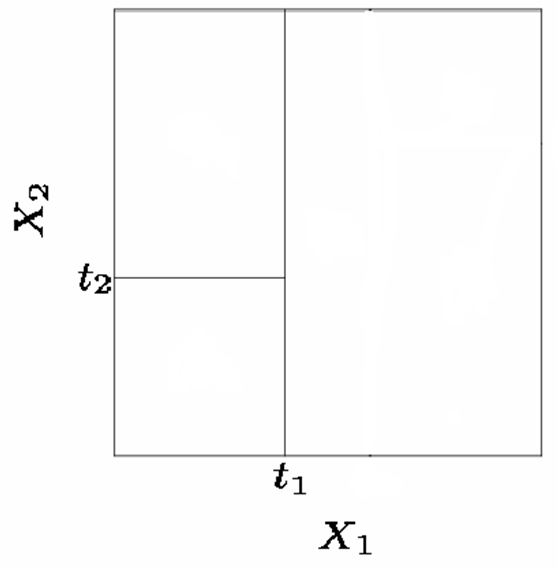
3. 만약 $X_{1} > t_{1}$이면, $X_{1} = t_{3}$을 분리합니다.

4. 만약 $X_{1} > t_{3}$이면, $X_{2} = t_{4}$를 분리합니다.

위의 방법들로 partitions를 생성할 때, 이것을 항상 tree structure를 사용하여 나타냅니다.
비전문가에게 모델을 설명하는 매우 간단한 방법입니다.

Another way of visualizing the decision tree
ISLR 내용을 바탕으로 요약 작성되었습니다.
'ISLR' 카테고리의 다른 글
| Chap 08 Bagging and Random Forests : Random Forests (0) | 2019.10.14 |
|---|---|
| Chap 08 Bagging and Random Forests : Bagging (0) | 2019.10.11 |
| Chap 06 선형 모델 선택 및 정규화 - Shrinkage Methods : Ridge, LASSO (9) | 2019.10.04 |
| Chap 06 선형 모델 선택 및 정규화 - Subset Selection (0) | 2019.10.02 |
| Chap 06 선형 모델 선택 및 정규화 - 최소 제곱법 보완 (0) | 2019.10.01 |




댓글