문제점
결정 트리는 높은 분산을 갖습니다.
즉, training data를 두 파트로 랜덤 하게 나누고 각각 결정 트리를 적합시키면 둘의 결과는 꽤 다르게 나옵니다.
낮은 분산을 갖는 모델을 만드는 것이 목표입니다.
이 문제를 해결하기 위해 bagging을 사용합니다. (bagging은 bootstrap aggregating에서 추린 말입니다.)
Bootstrapping?
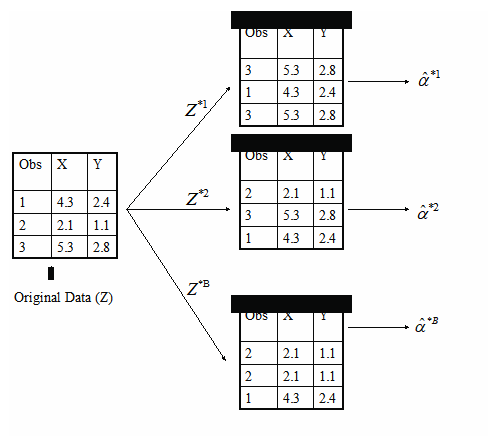
같은 사이즈의 관측된 데이터셋을 Resampling합니다.
Resampling 된 데이터셋은 원래의 데이터셋에서 중복 가능한 random sampling을 통해 만들어졌습니다.
Bagging?
Bagging은 아래의 두 개의 방법을 기반으로 한 매우 강력한 아이디어입니다.
Averaging : 분산을 줄입니다.
Bootstrapping : Training datasets의 수를 늘립니다.
Averaging은 분산을 어떻게 줄일 수 있을까요?
관측치의 집합을 averaging하는 것은 분산을 줄입니다.
확률 표본을 생각해보면 간단합니다.
표본 평균의 분산은 $\frac {\sigma^{2}}{n}$이고 확률변수의 분산은 $\sigma^{2}$인 것만 알면 됩니다.
Bagging 작동 방식
C 개의 다른 bootstrapped training datasets를 생성합니다.
통계 학습 방법을 C 개의 training datasets에 각각 훈련시키고 예측 결과를 확인합니다.
예측의 경우
회귀 : 모든 C trees로부터 얻은 모든 예측치의 평균
분류 : 모든 C trees의 사이에서 가장 다수인 것
회귀 트리에서의 Bagging
C개의 bootstrapped training datasets를 사용하여 C개의 회귀 트리를 만듭니다.
결과로 나온 예측치들의 평균을 구합니다.
트리들은 가지치기(prun)가 되어있지 않습니다. 따라서 각 트리는 높은 분산을 가지지만 편향은 낮습니다.
Averaging은 이 트리들의 분산을 줄여주어 결국에 분산과 편향이 모두 낮은 결과를 얻을 수 있습니다.
분류 트리에서의 Bagging
C개의 bootstrapped training datasets를 사용하여 C개의 분류 트리를 만듭니다.
각각의 bootstrapped data set이 예측한 class를 기록하고 가장 많이 발생하는 하나를 전반적인 예측으로 간주합니다.
다른 방법은 분류기가 확률 추정을 하게 되면 확률의 평균을 구한 다음 가장 높은 확률을 보인 class를 예측하면 됩니다.
두 방법 모두 성능이 좋습니다.
Error Rates 비교
초록색 선은 simple majority vote approach입니다.
보라색 선은 averaging the probability estimates입니다.
두 선 모두 sing tree(dashed red)보다 성능이 좋고 Bayes error rate(dashed grey)와 가깝습니다.

예시 1 : Housing Data
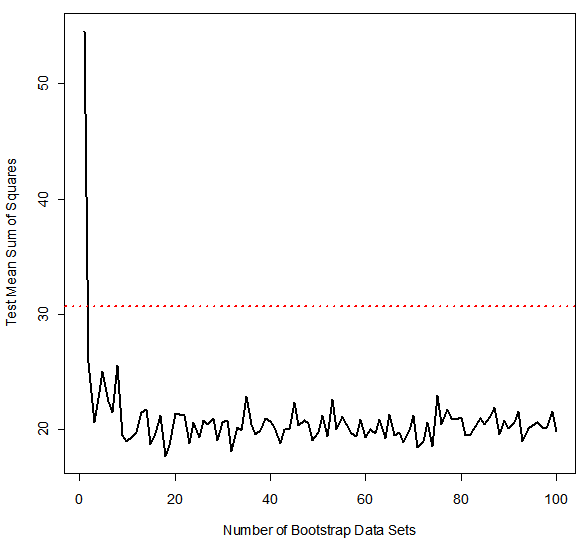
The red line은 singe tree를 사용한 test mean sum of squares입니다.
The black line은 bagging error rate입니다.
예시 2 : Car Seat Data
The red line은 singe tree를 사용한 test error rate입니다.
The black line은 majority vote를 사용한 bagging error rate이고 the blue line은 averages the probabilities입니다.

Out-of-Bag Error Estimation
Bootstrapping이 training data set을 만드는데 관측치의 부분집합을 랜덤 하게 포함하기 때문에 선택되지 않은 남은 부분이 testing data가 될 수 있습니다.
보통, 각각의 bagged tree는 관측치의 2/3을 사용하고 나머지 1/3은 testing을 위해 사용합니다.
변수 중요도 측정
Bagging은 전형적으로 single tree를 사용하는 것보다 예측 정확도를 개선시킵니다. 그러나 문제는 모델 해석이 어려워집니다.
몇 백개의 트리를 만들기 때문에 이제 어떤 변수가 가장 영향을 미치는지 더 이상 명확하지 않습니다.
따라서 bagging은 예측 정확도를 증가시키는 대신 해석력을 희생합니다.
하지만 Relative Influence Plots를 사용하여 각 예측변수에 대한 중요도의 전반적인 요약을 얻을 수 있습니다.
Relative Influence Plots
The response를 예측하는데 가장 중요한 변수가 무엇인지 어떻게 결정할 수 있을까요?
Relative influence plots라고 불리는 방법을 계산할 수 있습니다.
이 plots는 각 변수에 대한 점수를 제공합니다.
이 점수들은 특정 변수에서 분리했을 때 감소한 MSE를 나타냅니다.
숫자가 0에 가까울수록 변수는 중요하지 않음을 나타내고 제외할 수 있는 가능성이 있습니다.
더 큰 숫자의 점수일수록 변수가 가진 영향력이 더 큽니다.
예시 : Housing Data
Median Income이 가장 중요한 변수입니다.
Longitude, Latitude and Average occupancy는 다음으로 중요한 변수입니다.

'ISLR' 카테고리의 다른 글
| Chap 09 Support Vector Machines - The Support Vector Classifier (0) | 2019.10.15 |
|---|---|
| Chap 08 Bagging and Random Forests : Random Forests (0) | 2019.10.14 |
| Chap 08 트리 기반 모델 - Decision Trees : Regression Trees (0) | 2019.10.08 |
| Chap 06 선형 모델 선택 및 정규화 - Shrinkage Methods : Ridge, LASSO (9) | 2019.10.04 |
| Chap 06 선형 모델 선택 및 정규화 - Subset Selection (0) | 2019.10.02 |




댓글