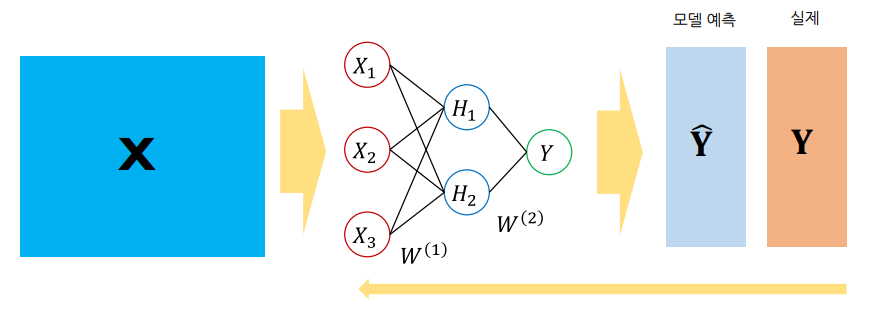
뉴럴네트워크
선형회귀모델?
Y가 연속형: 입력변수(X)의 선형결합으로 출력변수(Y)를 표현
$f(X) = w_{0}+w_{1}X_{1}+w_{2}X_{2}+...+w_{p}X_{p}$
로지스틱 회귀모델?
Y가 범주형: 입력변수(X)의 비선형결합(로지스틱 함수 형턔)로 출력변수(Y)를 표현
$f(X) = \frac{1}{1+e^{-(w_{0}+w_{1}X_{1}+w_{2}X_{2}+...+w_{p}X_{p})}}$
입력변수의 선형결합 후 선형결합 갑의 비선형 변환(Nonlinear transformation)

퍼셉트론(Perceptron)?
단층 퍼셉트론 - 초기 뉴럴네트워크(1957년 Frank Rosenblatt 개발)
입력값의 선형결합 값을 구하고 그 값이 0보다 큰지를 여부로 분류
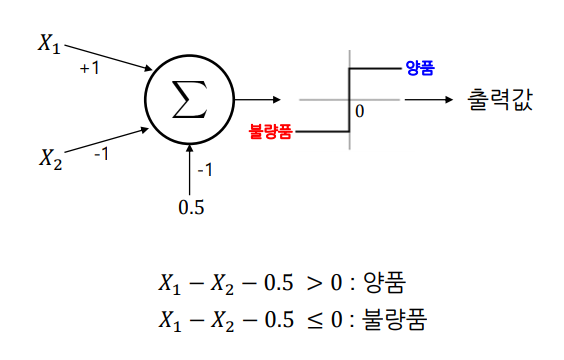
단순 퍼셉트론 예제?
XOR은 단층 퍼셉트론으로 못함
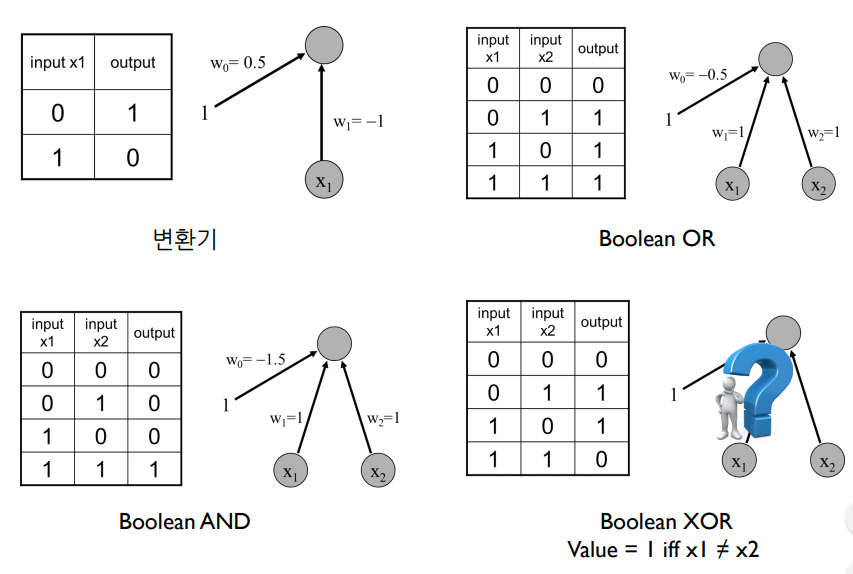
XOR은 선형으로 나눌 수 없음

2중 퍼셉트론?
두 개이 퍼셉트론을 결합(2중 퍼셉트론: 2-layer perceptron) = 뉴럴 네트워크
두 개의 입력변수와 한 개의 출력변수
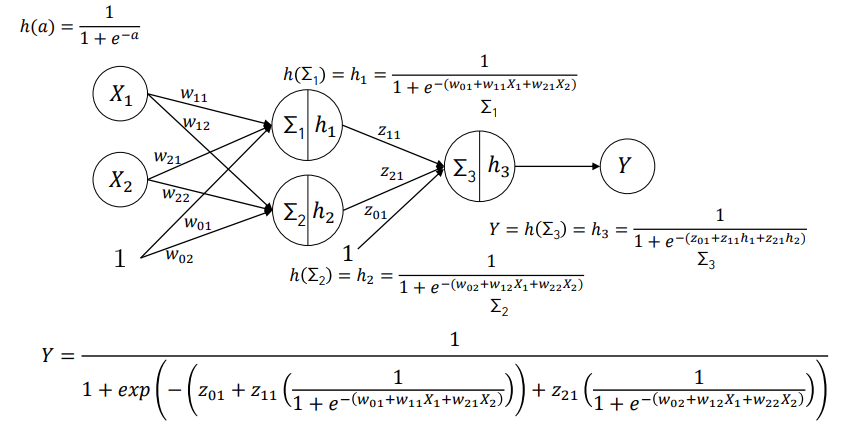
다층 퍼셉트론(Multilayer Perceptron)?
다층 퍼셉트론 -> 인공신경망(Artificial Neural Networks)
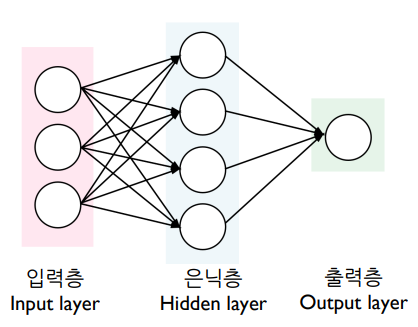
입력층 : 입력변수의 값이 들어오는 곳, 입력변수의 수 = 입력노드의 수
은닉층 : 은닉층에는 다수 노드 포함 가능, 다수의 은닉층을 형성 가능
출력층 : [범주형] 출력노드의 수 = 출력변수의 범주 개수, [연속형] 출력노드의 수 = 출력변수의 개수
선형회귀모델, 로지스틱회귀모델, 뉴럴네트워크모델?
선형회귀모델 : $f(X) = w_{0}+w_{1}X_{1}+w_{2}X_{2}$
로지스틱회귀모델 : $f(X) = \frac{1}{1+e^{-(w_{0}+w_{1}X_{1}+w_{2}X_{2})}}$
뉴럴네트워크 모델 : $f(X) = \frac{1}{1+exp(-(z_{01}+z_{11}(\frac{1}{1+e^{-(w_{0}+w_{1}X_{1}+w_{2}X_{2}}}))+z_{21}(\frac{1}{1+e^{-(w_{0}+w_{1}X_{1}+w_{2}X_{2}}}))}$
뉴럴네트워크 파라미터?
파라미터 : 층 간 노드를 연결하는 가중치 $(w_{11},...,z_{11})$ -> 알고리즘으로 설정
하이퍼파라미터 : 은닉층 개수, 은닉노드 개수, activation function -> 사용자가 임의로 결정

Activation Function(활성화 함수)?

Activation Function : Sigmoid function?
Logistic function, Sigmoid function, Squashing function (Large input → Small output)
아웃풋 범위: 0~1
인풋값에 대해 단조증가 (혹은 단조감소) 함수
미분결과를 아웃풋의 함수로 표현 가능 (Gradient learning method에 유용하게 사용) 중요함
$\frac{\text{d}\Phi(z)}{\text{d}z}=\frac{1}{1+e^{-z}}(1-\frac{1}{1+e^{-z}}=\Phi(z)(1-\Phi(z))$
뉴럴네트워크 파라미터 결정, 비용함수?
뉴럴네트워크 모델로부터 나온 Y값과 실제 Y값의 차이를 최소로 하는 가중치
$\arg\min_{w} \sum_{i}L(Y, f(X;w))$
뉴럴네트워크 비용함수 - 수치예측?
예측값과 실제값의 차이를 측정하는 방법
Regression: mean squared error (MSE) $L = \frac{1}{2}(o-t)^{2}$ (o:예측값, t:실제값)
미분가능해야 함
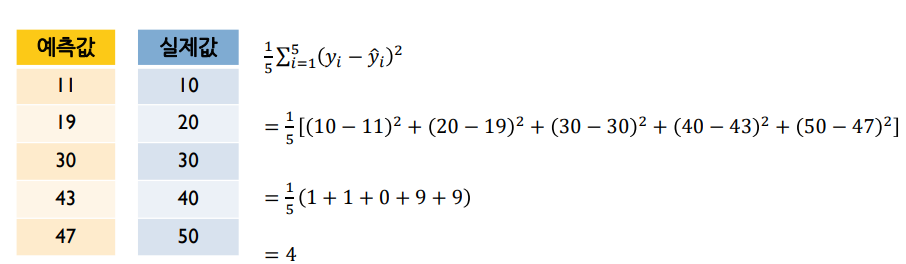
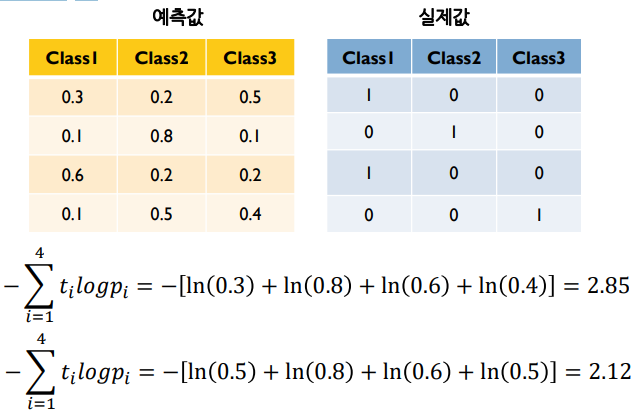
뉴럴네트워크 비용함수 – 분류?
예측값과 실제값의 차이를 측정하는 방법
Classification: cross entropy $L = -\sum_{i}t_{i}logp_{i}$
미분가능해야 함
뉴럴네트워크 학습 - 경사하강법?
Gradient: 함수의 기울기
Gradient descent method: a first-order optimization algorithm
Optimization: 함수의 최솟값 혹은 최댓값을 찾는 과정
“Turning points” 의 개수는 함수의 차수에 의해 결정
모든 turning point가 최솟값 혹은 최댓값은 아님
최솟값들 중 가장 작은 최솟값: 전역 최솟값 (global minimum)
지역적인 최소값: 지역 최소값 (local minimum)

경사하강법 (Gradient Descent Method)
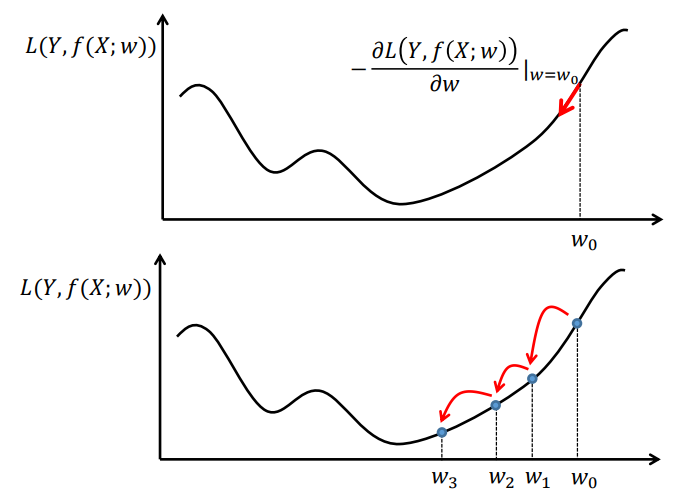
$w_{t+1} = w_{t} - \alpha \cdot L'(w_{t})$
$0 < \alpha < 1$ : learning rate
좀 더 섬세하고 촘촘히? Small $\alpha$
좀 더 빠르게? Large $\alpha$

경사하강법 예제?
$L(w) = w^{4}$
$\alpha$ : learning rate
$w_{0} = 2$, $\alpha = 0.01$
$w_{1}=w_{0}-\alpha L'(w_{0})=1.6800$
$w_{2}=w_{1}-\alpha L'(w_{1})=1.4903$
$w_{3}=w_{2}-\alpha L'(w_{2})=1.3579$
$\ldots$
$w_{200}=w_{199}-\alpha L'(w_{199})=0.2461$
$\alpha=0.02$로 하면? 좀 더 빠르게 줄어듦


댓글