# Code source: Jaques Grobler
# License: BSD 3 clause
코드 소스와 저작권은 위와 같음을 밝힙니다.
import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets, linear_model
from sklearn.metrics import mean_squared_error, r2_score
%matplotlib inline
필요한 모듈을 가져옵니다.
# Load the diabetes dataset
diabetes = datasets.load_diabetes()
datasets의 당뇨병 데이터를 불러옵니다.

참고로 sklearn의 datasets은 그림1과 같습니다.
만일 다른 dataset을 불러오고 싶다면 변수명과 load_(불러오고 싶은 데이터셋 이름)을 바꿔주면 됩니다.
boston = datasets.load_boston()
boston 데이터셋을 불러오는 코드입니다.

당뇨병 데이터셋을 살펴보겠습니다. Samples total이 442고 Dimensionality가 10이니 (442 X 10) 행렬입니다.
Features(X or data)는 실수이며 -.2에서 .2사이이고 Targets(y or target)은 정수이며 25에서 346사이의 숫자로 이루어져있습니다.
diabetes
실제 코드를 치면 그림3과 같은 결과가 나옵니다.
# Use only one feature
diabetes_X = diabetes.data[:, np.newaxis, 2]
data의 한 열을 골라 X로 써줄 것입니다.
diabetes.data[:, np.newaxis, 2]에서 ':' 는 전체 행을 가져오고 'np.newaxis'로 차원을 하나 늘려준 후 '2'로 3번째 열의 데이터를 가져오게 됩니다.
2인데 3번째 열을 가져오는 이유는 0부터 세기 때문입니다.
결과적으로 diabetes_X는 (442 X 1) 행렬입니다.
코드로 확인해보면
diabetes_X.shape
# Split the data into training/testing sets
diabetes_X_train = diabetes_X[:-20]
diabetes_X_test = diabetes_X[-20:]
diabetes_X를 train set과 test set으로 나누어 주겠습니다.
Train set은 처음부터 -19까지(마지막은 python이 포함시키지 않습니다) Test set은 -20부터 끝까지입니다.
각각의 행렬은 어떻게 될까요?
맨 처음 (442 X 1) 행렬이었으니 마지막 20개를 나눠주면 (422 X 1), (20, 1) 행렬이라고 추측할 수 있습니다.
확인해 보면
print(diabetes_X_train.shape)
print(diabetes_X_test.shape)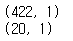
역시 그러합니다.
# Split the targets into training/testing sets
diabetes_y_train = diabetes.target[:-20]
diabetes_y_test = diabetes.target[-20:]
diabetes_y도 X와 마찬가지로 데이터 셋을 나누어줍니다.
# Create linear regression object
regr = linear_model.LinearRegression()

sklearn의 선형 모델 중 선형회귀를 사용하겠습니다. 선형회귀의 설명은 그림6과 같습니다.
당뇨병 데이터에서 Parameter를 조정해야 할 부분은 딱히 없습니다.
# Train the model using the training sets
regr.fit(diabetes_X_train, diabetes_y_train)
위에서 만든 선형 회귀 모델에 diabetes_X_train, diabetes_y_train 데이터를 적합시킵니다.
# Make predictions using the testing set
diabetes_y_pred = regr.predict(diabetes_X_test)
Train 데이터로 만들어진 회귀 직선에 diabetes_X_test라는 새로운 X를 넣어주어 y를 예측합니다.
# The coefficients
print('Coefficients: \n', regr.coef_)
# The mean squared error
print("Mean squared error: %.2f"
% mean_squared_error(diabetes_y_test, diabetes_y_pred))
# Explained variance score: 1 is perfect prediction
print('Variance score: %.2f' % r2_score(diabetes_y_test, diabetes_y_pred))
모형 결과를 해석해 보겠습니다.
regr.coef_로 회귀 계수를
mean_squared_error로 MSE 값을
r2_score로 $R^{2}$ 값을 구할 수 있습니다.
.2f는 소수점 둘째자리까지 나타내라는 뜻입니다.
# Plot outputs
plt.scatter(diabetes_X_test, diabetes_y_test, color='black')
plt.plot(diabetes_X_test, diabetes_y_pred, color='blue', linewidth=3)
plt.xticks(())
plt.yticks(())
plt.show()
plt.scatter는 산포도를 그려줍니다. diabetes_X_test, diabetes_y_test에 해당하는 점을 검은색으로 표시합니다.
plt.plot는 라인(line)그래프를 그려줍니다. diabetes_X_test, diabetes_y_pred에 해당하는 선을 파란색으로 굵기는 3으로 표시합니다.
plt.xticks(()), plt.yticks(())는 눈금을 나타내는 명령어입니다. 여기선 빈칸 괄호를 넣어주므로 눈금을 표시하지 않습니다.
plt.show는 그래프를 보여줍니다.

코드 원문 링크를 첨부합니다.
Linear Regression Example — scikit-learn 0.21.3 documentation
Note Click here to download the full example code Linear Regression Example This example uses the only the first feature of the diabetes dataset, in order to illustrate a two-dimensional plot of this regression technique. The straight line can be seen in t
scikit-learn.org
'scikit-learn' 카테고리의 다른 글
| Scikit-Learn(사이킷런) 코드 완벽 분석 - Tree Regression (1) | 2019.10.22 |
|---|---|
| Scikit-Learn(사이킷런) 코드 완벽 분석 - Linear Regression OLS, Ridge Variance 비교 (0) | 2019.10.21 |
| Scikit-Learn(사이킷런) 코드 완벽 분석 - Linear Regression Lasso (0) | 2019.10.18 |
| Scikit-Learn(사이킷런) 코드 완벽 분석 - Linear Regression Ridge (0) | 2019.10.16 |
| Scikit-Learn(사이킷런) 소개 (0) | 2019.10.16 |



댓글