Dimensionality Reduction
Dimensionality Reduction?
관점은 분산 표상 이전의 시점
데이터는 전부 Bag-of-Words 방식
BOW로 표현된 다큐먼트는 굉장히 많은 변수들로 이루어져 있음(term, words, token)
일부분만이 텍스트 분석 태스크에 대해 관련이 있음(전처리를 거치게 되면)
TDM 형태 : Term이 행이고 Documents가 열인 형태
이 데이터가 가지고 있는 문제점
첫 번째 : 차원이 큼, 보통 일반적으로 tem의 개수가 document개수보다 많음
통계학적인 관점에서 보면 관측치의 수가 변수의 수보다는 많아야 다중공선성같은 여러 통계적 가정을 만족을 할 가능성이 있음
그런데 변수에 수가 객체 수 또는 관측치 수보다도 더 많으면 전통적인 통계적인 방법을 사용하기엔 무리임
해당하는 가정들을 전부 만족시킬 수가 없기 때문임
두 번째 : 연산 그리고 효율성 관점에서 봤을 때 문제점, sparseness
이 데이터 매트릭스의 대부분의 요소가 0임
왜냐하면 term의 개수는 가지고 있는 언어에서의 전체 단어 수 또는 토큰의 수 라고 표현을 할 때, 한 문서는 정말로 긴게 아닌 이상 paragraph같은 경우에 100~200단어 정도로 구성이 되고 영어가 13만 개 정도의 단어가 있는데 그 중에 100개 빼고 나머지의 값은 전부 0이 됨
저장과 처리에 있어서 매우 비효율적인 문제가 발생
Dimensionality Reducton 핵심?
1. 계산 효율성을 높이는 것 : 타임 세이브, storage와 network resources 세이브
2. 무작정 효율성만 추구하는게 아니라 가능하다면 텍스트 마이닝 또는 텍스트 분석 결과물의 질을 높임 : 분류 정확도 향상, 클러스터 간의 modularity 향상, 일정한 퍼포먼스를 얻어내기 위해서 훈련 데이터의 수를 줄임 등
효율적으로 계산 및 분석 결과물 품질도 높임
Dimensionality Reduction 구분?
DTM 형태(행이 D, 열이 T)을 홀쭉하게 줄임
T의 크기가 T 프라임보다 크게 만듦
첫 번째 방식 : Feature Selection
두 번째 방식 : Feature Extraction
Feature Selection : 주어진 변수 둘 중에서 유의미 할 것으로 판단되는 일부분을 부분 집합으로 선택
오리지널 변수가 그대로 남아 있으면서 중요한 변수만 뽑힘
Feature Extraction : 주어진 오리지널 변수들을 가지고 해당하는 데이터 셋의 특징을 잘 보존하는 새로운 소수의 변수 집합을 찾아냄
둘의 차이는 selection은 x가 x 프라임이라는 변수 집합으로 만들어진다면
extraction은 x가 z라는 완전히 새로운 변수 집합으로 바뀜
Selection 관점에서 보자면 두 가지의 가능한 방법론이 있음
Filter, Wrapper
Filter : 원타임, 특정 기준에 따라서 그 기준을 만족하는 설명 변수들을 선택하는 방식
Wrapper : 중간에 알고리즘 있어서 해당하는 알고리즘의 피드백을 받아 중요한 변수들을 반복적으로 가장 최적의 조합이 되도록 찾아 가는 부분
selection 관점에서 classification 문제라고 할 때 Filter와 Wrapper의 가장 큰 차이점은 러닝 알고리즘이 사용되지 않으면 필터, 사용이 되면 Wrapper
클래스 레이블은 모두가 다 사용
Extraction같은 경우에는 데이터가 가지고 있는 특성이 어떻게 정의가 되느냐에 따라서 데이터 전체가 가지고 있는 variance를 최대로 보전(분산 최대 보전) : 주성분 분석
각각의 개체들 간의 거리 정보를 최대한 보존 : 사회 과학 쪽에서도 많이 쓰이는 mds(Multidimensional scaling, 다차원척도법)
잠재적인 structure 뽑아내면 Latent semantic indexing가 됨
이 방식들은 전부 비지도 학습 방식
원 데이터의 x만 사용 클래서 레이블 당연히 쓰지 않음, 학습 알고리즘에도 독립적음
Dimensionality Reduction Feature selection vs feature extraction 구체적으로?
변수의 문자열을 잘보기
Selection은 선택이 되었을 때 v의 개수가 준거지 v라는 문자열 자체는 바뀌지 않음
Extraction은 오리지날 데이터로부터 new set of features를 만들어냄, 변수의 개수 줄고 v라는 문자열이 z라는 문자열로 바뀜, 어떤 오리지날 변수들의 조합으로써 새로운 변수가 만들어짐
Filter vs Wrapper?
Filter : feature selection알고리즘이 학습 알고리즘의 또는 모델의 영향을 받지 않음
Wrapper : 변수가 한 번 줄은 다음에 최종적으로 다운스트림 태스크를 수행하는 알고리즘한테 물어봄, 적합한 조합인가? 라는 질문에 아닌데 더 있을 것 같은데라는 피드백을 주면 다시 한 번 더 찾아서 넘겨줌, 피드백을 또 주고 넘겨주는 이 과정을 충분히 하는 feedback 루프가 있음
Feature Selection
Artificial Data Set?
10 Documents with 10 Terms
TDM
Binary classification
6 positive documents & 4 negative documents

Positive와 Negative를 잘 구분하기 위해서 가장 중요한 Term이 무엇인가 찾음
두 범주를 구분을 하려면 상식적으로는 해당하는 텀이 한쪽 범주에만 몰아서 등장을 하고 반대쪽 범주에는 등장을 하지 않는게 좋음
이런 관점에서 봤을 때는 계산을 하지 않더라도 1번 term의 경우 postive 범주에 주로 등장
2번 term의 negative 범주에만 등장
이 두개는 아마도 중요 할 가능성이 높을 것
3번은 postive, negative 다 등장, 어떤 지표 사용해도 중요도가 낮을 가능성이 높음
나머지 열 개 term들에 대해서도 상대적으로 순위를 매겨
Feature Selection 관점에서 Document frequency(DF)?
총 10가지의 선택할 수 있는 matrix 설명
당연히 뒤로 갈수록 계산 양은 더 많아짐 대신에 변별력 높아짐
앞쪽은 단순하지만 변별력이 그리 높지 않을 가능성 큼
첫 번째 지표 : Document frequency(DF)
특정한 단어가 등장한 document의 수 $N_{D} (w)$가 됨
Term 1 : DF(w) = 6
Term 2 : DF(w) = 4
Term 3 : DF(w) = 10
Document frequency가 높다고 했을 때 classification 변별력이 높은가의 논리적인 과정의 절차는 틀렸다고 볼 수 있음
세 번째 단어같은 경우에는 DF가 가장 높은데 변별력은 0이기 때문에 무작정 DF가 높은 게 좋은 건 아님
Filter 방식 관점에서 Accuracy(Acc)?
해당하는 단어만 가지고(이 단어의 존재유무만을 가지고) 분류기 만든다고 했을때 얼마나 잘 분류가 될 것인가라는 개념
positive 기준으로 봤을때 N(Pos,w) w라는 단어가 들어있는 positive 문서의 개수 마이너스(-) N(neg,w) w가 들어가 있는 negative 문서의 개수를 계산
Term 1의 경우 Postive는 6개 negative는 0 : 6-0=6
Term 2 : 0-4 = -4
Term 3 : 6-4=2
1번이 3번보다 더 중요하다 판별
3번과 2번을 비교했을 때 음수 값 때문에 문제가 되는 상황이 발생
특정 범주에는 유리하지만(positive) negative 범주에는 불리한지 아닌지 지표
Feature Selection 관점에서 Accuracy ratio(AccR)?
전체 긍정 positive문서 중에 w단어가 존재는 비율 - negative 문서 중에 w 단어가 존재하는 비율한 다음에 절대값 씌움
Term 1은 6/6=1, 0/4=0, |1-0|=1
Term 2는 0/6=0, 4/4=1, |0-1|=1
Term 3은 6/6=1, 4/4=1, |1-1|=0
Term 1과 2의 중요도는 같지만 Term3 중요도는 매우 낮게 됨
Feature Selection 관점에서 Probability Ratio(PR)?
AccR에서 -가 아닌 /를 해줌
Term 1 : 1/0, 무한대
Term 2 : 0/1, 0
Term 3 : 1/1, 1
좋은 지표는 아님
계산 결과?

범주에 상관없이 변별력이 클수록 높은 값이 나오는 것은 AccR라고 볼 수 있음
1번 2번이 매우 크게 나옴
4번 5번 6번 7번 같은 경우에도 1,2번 만큼은 아니어도 상대적으로 변별력을 가지고 있음
해당하는 part 잘 설명을 해주는 것을 파악
Feature Selection 관점에서 Odds ratio(OddR)?
Odds : 성공하지 못할 확률 분의 성공할 확률
성공할 확률 : p
Odds = p/(1-p)
OddR(w) : negative Odds분의 positive Odds 비율
Term 8하고 9구분
Term 8 : 3/2, 2/3, 1
Term 9 : 3/1, 3/3, 3
9번 Term이 8번 Term보다는 범주 구분에 있어 변별력 더 클 것
Feature Selection 관점에서 Odds ratio Numerator(OddN)?
OddR에서 분자만 뽑음
8번 Term은 3, 2, 6
9번 Term은 3, 3, 9
여전히 대소 관계 크게 잘 유지됨
Feature Selection 관점에서 F1-Measure?
어떤 특정한 단어를 가지고 confusion matrix를 만들었을 때 confusion matrix를 기준으로 recall과 precision 계산 가능
Recall(w) : N(Pos, w)/ (N(Pos, w)+N(Pos, $\bar{w}$))
Precision(w) = N(Pos, w)/ (N(Pos, w)+N(Neg, w))
Recall(w)과 Precision(w)의 조화평균이 F1-Measure
negative fatures가 평가절하 된다는 뜻은 positive 범주를 기준으로 계산하기 때문
Term 1 : 2*6/(6+6)=1
Term 2 : 2*0/(6+4) = 0
Term 3 : 2*6/(6+10)=0.75
특정한 범주를 기준으로 했을 때 F1-measure는 그리 좋은 평가지표가 아님
계산 정리?

Positve 범주들에 대해서는 높은 값을 부여하고 있지만 Negative 범주를 잘 구분해 내는 Term2에 대해서는 상대적으로 낮은 값을 가짐
비대칭성인 특징을 가진 지표들
Feature Selection 관점에서 Information Gain(IG)?
대칭적인 지표
어떤 feature가 주어졌는지, 주어지지 않았는지에 따른 entropy 차이 감소분을 계산
어떤 w라는 단어에 등장 유무가 주어지지 않았을 때 엔트로피는 범주 2개니까 $\sum_{C=\left\{Pos,Neg\right\}} -P(C) \times log(P(C))$
w가 주어졌을 때는 $p(w)\left[\sum_{C=\left\{Pos,Neg\right\}} -P(C|w) \times log(P(C|w))\right]+p(\bar{w})\left[\sum_{C=\left\{Pos,Neg\right\}} -P(C|\bar{w}) \times log(P(C|\bar{w}))\right]$
IG(w)=Entropy(absent w) - Entropy(given w)
엔트로피라는게 불확실성이 기 때문에 어떤 단어가 두 범주를 구분하는데 있어서 정보량을 크게 가지고 있다면 IG는 앞에 있는 부분이 뒤에 있는 부분보다 클 것이고 IG도 커질 것
Term 1 예시?
-0.6 * log(0.6) - 0.4 * log(0.4) = 0.29
0.6[-1 * log(1) - 0 * log(0)] + 0.4[-0 * log(0) - 1 * log(1)] = 0, log(0)은 0으로 convert, w란 데이터의 존재유무만 가지고 있어도 불확실성 없이 완벽하게 구분
IG(w) = 0.29 - 0 = 0.29
Feature Selection 관점에서 Chi-squared statistic?

w라는 단어의 출현 여부와 긍정/부정에 대한 클래스가 만약에 통계적으로 완벽하게 독립이라면 기대값을 계산 가능
만약에 w 등장의 확률이 60%이고 긍정 문서의 확률이 60%였으면
w가 포함된 긍정문서문서는 10분의 6 곱하기 10분에 6이니까 약 3.6 개가 등장(만약에 w가 포함된 것이냐 아니냐에 대한 유무와 부정/긍정 범주가 독립이라는 가정을 했을 때)
Term 4에서는 w는 등장 문서 8개 등장 안한 문서 2개
긍정 문서는 6건 부정문서는 4건
기댓값 계산해보면 (1,1)은 4.8, (1,2)은 3.2, (2,1)은 -1.2, (2,2)는 0.8
Term 1에 대한 제곱합이 Term 4에 대한 제곱합보다 훨씬 큼
어느 범주를 기준으로 했느냐에 대해서 영향을 받지 않음
Feature Selection 관점에서 Bi-Normal Separation(BNS)?

누적 확률 분포에 대해서 해당하는 정보들을(x 값에 대응하는 지표) 찾아다가 그 값을 씀
w가 주어졌을 때의 positive 범주는 100%
w가 주어졌을 때 negative 범주는 50%
누적 확률 분포가 1이 되는 값이 어디냐라고 하면 0.9995
누적 확률 분포가 0.5 가 될 값이 어디냐라고 하면 0.5
1의 값은 이제 무한대로 가야 되니까 양쪽 극단을 0.0005를 빼거나 더해 줌
x 값을 찾으면 3.29, 0 둘 사이의 차이인 3.29가 해당하는 term의 중요도
정규분포를 가정을 하고 누적 확률 밀도 함수에 대해서 함수 값을 갖는 x 값을 찾아서 그 차이의 절대 값을 사용
훨씬 덜 알려져 있지만 이 논문을 쓴 저자들이 제안한 방법은 좋다 라는 걸 어필하기 위함
실험 결과를 보면 퍼포먼스 상당히 좋게 나옴
계산?

Term 1과 Term2는 모두 높은 값
지표 내부에서의 값만 보면 됨
Term 3과 Term 8같은 경우에는 전부 0의 값으로 제대로 판별
분산 표상 방식을 많이 쓰기 때문에 이런 전통적인 Term 또는 변수를 선택하는 방식을 많이 쓰지는 않지만 이런 상황에서 굳이 추천을 해야한다고 하면 IG와 카이 제곱 두가지 정도만 사용해도 괜찮음
Feature Selection 요약?
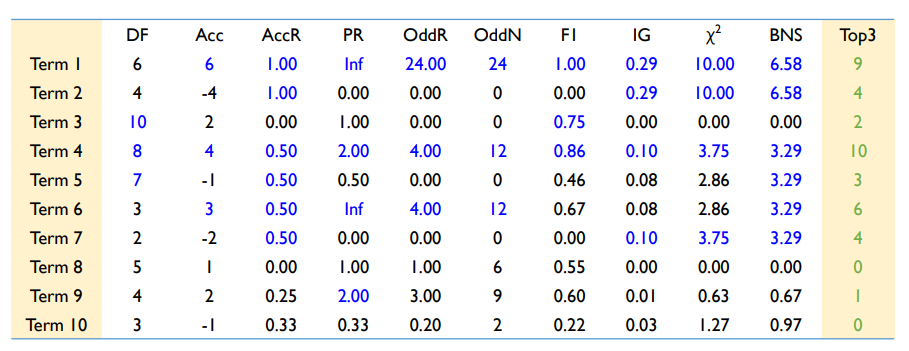
Term4는 모든 지표들에 대해서 가장 중요하다고 판정
DF는 유용한 지표가 아님
IG와 카이제곱을 중요하게 봐야 함
Empirical Study?
229 text classificaiton(노력 가상)
SVM이 base classifier
SVM이 기본적으로 bi이기 때문에 one-against-all method로 문제 풀어냄
Acc부터 BNS, Chi, IG 등이사용됨
Pow, Rand도 있음
BNS이 대부분 Best
총 500~1000차원 정도의 데이터 셋일 때
IG 통해서 변수 선택을 했을 때 약간의 성능 향상이 있었음
논문 저자들의 방법론의 굉장히 치우쳐져 있는 해석


댓글