Pruning a Tree
The training set에는 좋은 예측력을 자랑하지만 data에 overfit 되어있습니다.
data에 overfit되면 test set 예측 성능면에서 좋지 못합니다.
적은 분리의 작은 트리는 bias를 높이는 대신 분산을 낮춰 좋은 해석이 가능하도록 합니다.
이를 만들기 위한 방안은 각 분리마다 RSS 감소가 임계점을 초과할 때만 트리를 성장시키는 것입니다.
이 전략은 더 작은 나무를 만들지 몰라도 너무 short-sighted 합니다.
처음 보기엔 쓸모없는 분할일지 몰라도 나중엔 좋은 분할로 이어질 수 있습니다(후에 RSS를 크게 줄이는).
더 나은 전략은 매우 큰 트리 $T_{0}$를 만든 후 subtree로 가지치기를 하는 것입니다.
직관적으로 가장 작은 test error rate를 보이는 subtree를 선택하면 됩니다.
Test error은 cross-validation이나 validation set approach를 이용하여 측정할 수 있습니다.
CV를 쓰기엔 너무나 많은 가능한 subtree가 존재합니다.
대신에 작은 subtrees들의 집합을 선택할 수 있는 방안을 고려합니다.
Cost Complexity Pruning
Cost complexity pruning 또는 weakest link pruning로 알려진 방법을 사용합니다.
모든 가능한 subtrees를 고려하기보다는 nonnegative tuning parameter $\alpha$를 이용한 일련의 트리를 고려합니다.
Subtree T $\sqsubset $ $T_{0}$에 대응하는 $\alpha$의 값을 고려합니다.
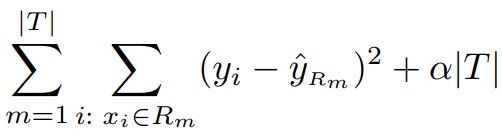
위의 식을 가능한 작게 만듭니다.
$\mid T \mid$는 Tree T의 terminal nodes의 수를 나타냅니다.
$R_{m}$은 m번째 terminal node에 대응하는 predictor space의 부분집합입니다.
$\hat {y_{R_{m}}}$은 $R_{m}에 속하는 training 관측치의 평균입니다.
Choosing the Best Subtree
The tuning parameter $\alpha$ subtree의 복잡도와 training data를 적합시키는 사이에서 trade-off를 통제합니다.
Optimal value $\alpha$를 cross-validation을 이용하여 선택해야 합니다.
Full data set을 가지고 $hat {\alpha}$에 해당하는 subtree를 획득합니다.
$\alpha$가 0이라면 subtree T는 $T_{0}$과 같습니다. 따라서 위의 식은 training error를 측정하는 것과 같아집니다.
$\alpha$가 증가할수록 많은 terminal nodes를 가진 tree를 생성하는 비용이 있으므로 위 식은 저 작은 subtree를 위하여 최소화하려는 경향이 있습니다.
Summary: Tree Algorithm
The training data를 가지고 recursive binary splitting을 사용하여 큰 트리를 만듭니다.
최소한의 관측치보다 작은 값을 가질 때까지 terminal node를 분리합니다.
만들어진 트리에 cost complexity pruning을 적용하여 best subtrees를 획득합니다. $\alpha$ 함수를 사용합니다.
$\alpha$를 선택하기 위해 K-fold cross-validation을 사용합니다. k = 1, ..., K
The k-fold를 제외한 $\frac {K-1}{K}$ 비율의 training data로 위 과정을 반복합니다.
$\alpha$ 함수로 남은 kth fold 데이터의 mean squared prediction error를 측정합니다.
결과의 평균을 구하고 평균 에러를 최소화하는 $\alpha$를 선택합니다.
선택한 $\alpha$값에 대응하는 subtree를 사용합니다.
Baseball Example
랜덥하게 data set을 절반으로 분리합니다. the training set에는 132개의 관측치를 the test set에는 131개의 관측치를 생성합니다.
The training data을 가지고 큰 regression tree를 만든 후 다양하게 $\alpha$를 조정하여 다른 수의 terminal nodes를 가진 subtree를 만듭니다.
$\alpha$함수로 트리의 the cross-validated MSE를 측정하기 위해 six-fold cross-validation을 수행합니다.
132개의 관측치가 6으로 떨어지기에 six-fold creoss-validation을 골랐습니다.

가지치기를 하지 않은 전체 tree입니다.

초록색 커브는 CV error as a function of the number of leaves입니다.
오렌지색 커브는 the test error입니다.
The CV error는 the test error의 합리적인 근사치입니다.
The CV error는 three-node tree를 취하고 test error도 three-node tree에서 깊어집니다.
Three terminal nodes를 포함한 가지치기된 트리는 다음과 같습니다.

ISLR 내용을 바탕으로 요약 작성되었습니다.




댓글